Package drop test

Several methods to represent fluids exist within LS-DYNA. Apart from the ICFD, ALE and CESE solvers, there are also meshless methods that can be used. For this case study, it has been chosen to explore the performances of the SPH and DES methods. The ability of SPH to represent fluids has been explored in other case studies on this site, e.g. a tank sloshing example, whereas the abilities of the computationally efficient DES solver are perhaps more unknown.
Fluid representation
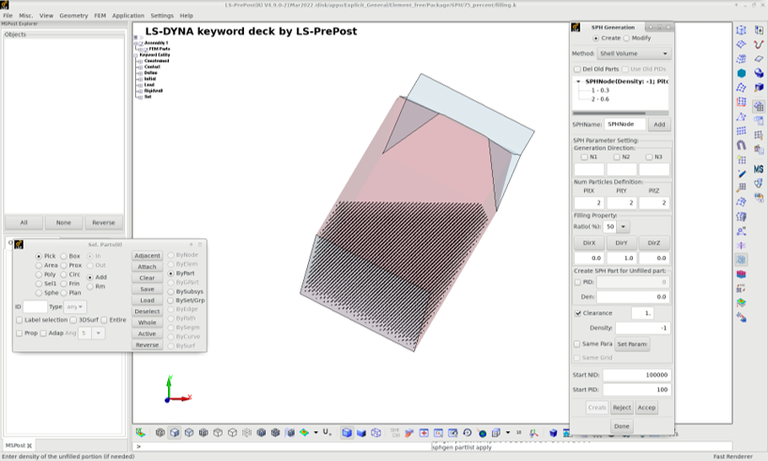
Starting with the SPH description of the fluid, this input is rather straightforward. Physical properties are assigned, viscosity and density on *MAT_NULL and speed of sound for water on e.g. *EOS_GRUNEISEN. A standard node-to-surface contact can be used for the contact with the carton, in this case it has been chosen to model it without friction or damping. Generation of the SPH particles is also a simple operation through the use of the SPH generation tool in LS-PrePost shown on the right hand side.
In the DES (Discrete Element Spheres) method, the bulk behavior of a material is entirely described by the interaction between rigid spheres. By changing the friction, rolling friction and cohesion between the particles, different bulk behavior can be achieved. In this case study, water-like properties have been achieved by setting the friction between the particles very low.
It may also be noted that since there are some spaces between the DES particles, an upscaling of the particles' density is required. The random packing rate of equally sized spheres is around 63.5 %, which is used in this case according to the equation below. However, the optimal packing rate is a bit higher, about 74%, which means that one should perhaps consider using a higher value since the packing rate after settling is likely higher than the random packing rate.
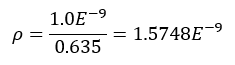
Step 1: Settling simulation

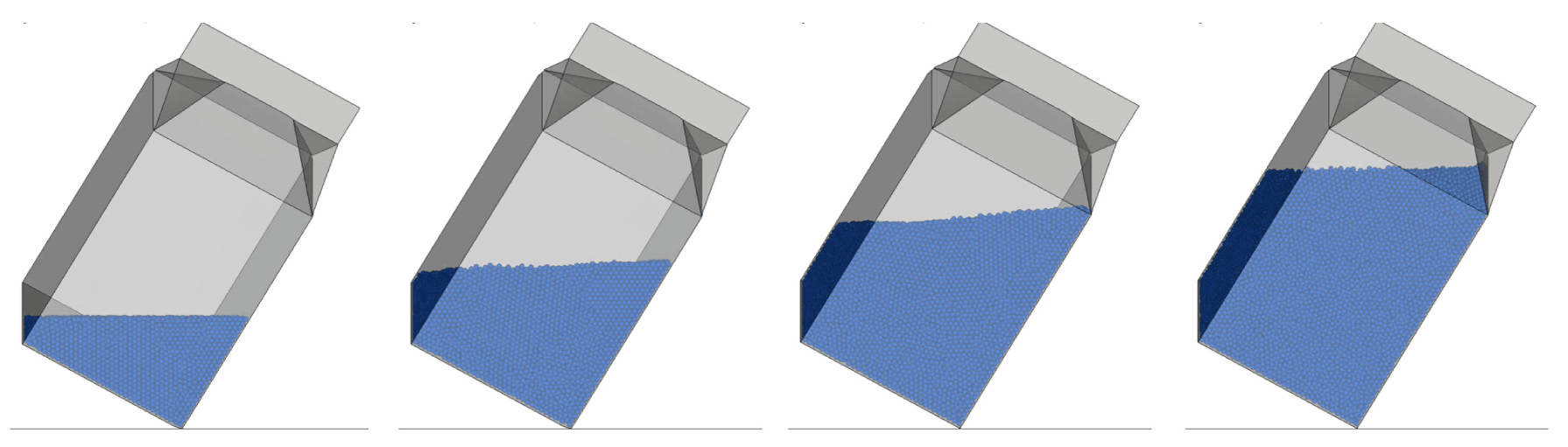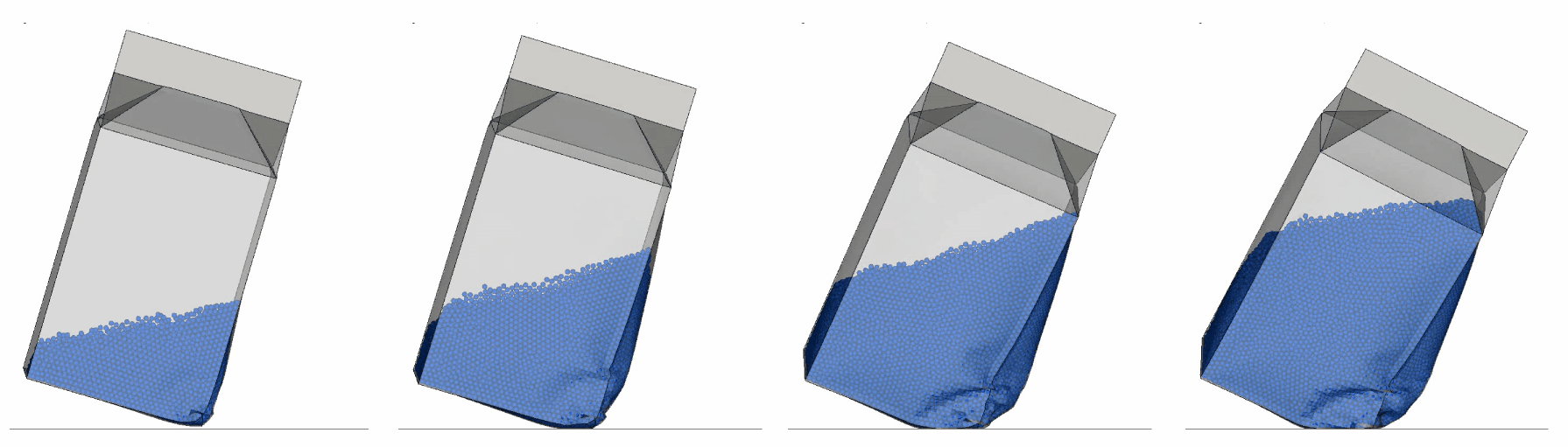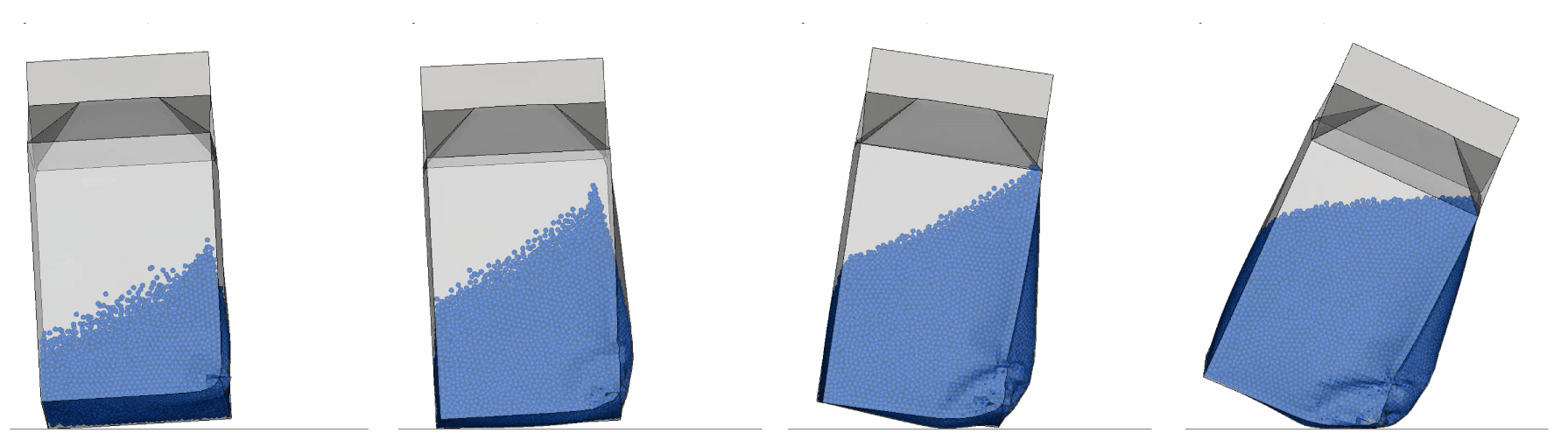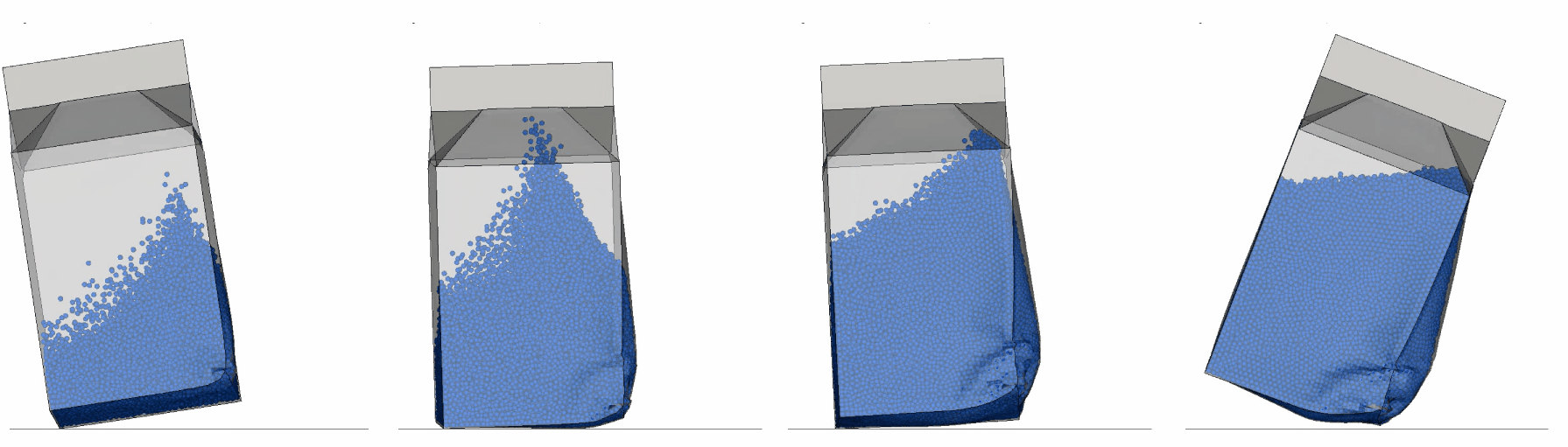
For both the SPH and the DES model, settling simulations are performed, in which the fluid is allowed to be packed and settle under gravity load.
For the DES method, where the particles have been randomly generated in a closed volume by a packing algorithm in LS-PrePost, there are more spaces in the initial configuration. Therefore, more packing and a longer time to a steady-state are to be expected in the pre-simulation, as can be seen in the animation to the left. A trick to faster reaching the steady-state is to increase the particle-to-particle damping in this stage. Since the friction is so low, the damping can be set as high as 99%.
Step 2: Drop simulation
After the initialization, drop tests are straightforward to perform. Below, animations of the drop test are shown for different filling rates using the DES description of the water.
But more interestingly, how do the results compare between the two methods? You may note a slight difference in the filling rate in the illustration to the right. The SPH water level is slightly higher and there is also possibly an effect from scaling the DES element densities, which leads to the mass of the SPH case being about 10% higher. Despite this, the behavior is quite similar.
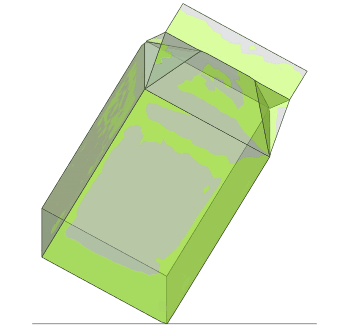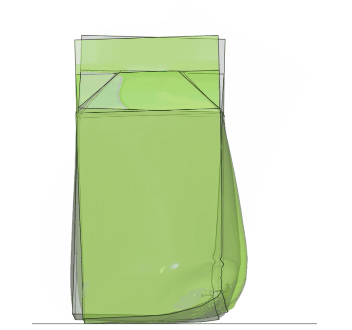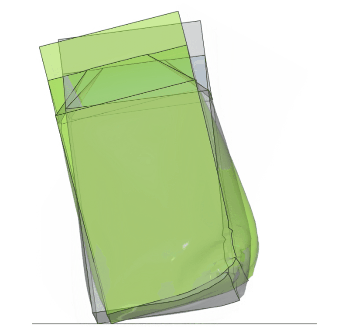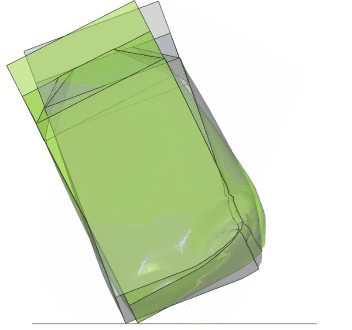
An overlay animation also confirms that the results are comparable; the DES model is gray and the SPH model green.
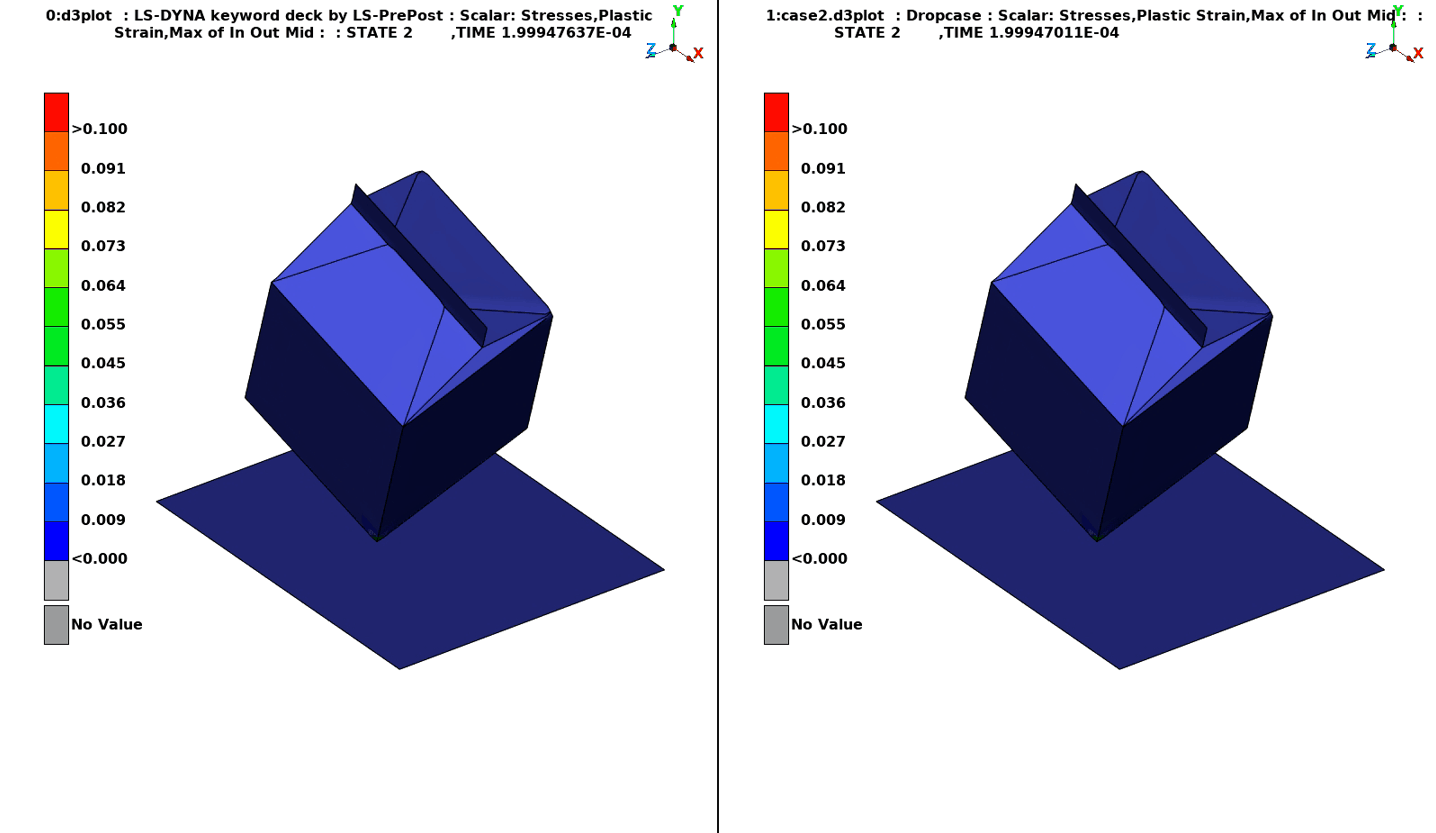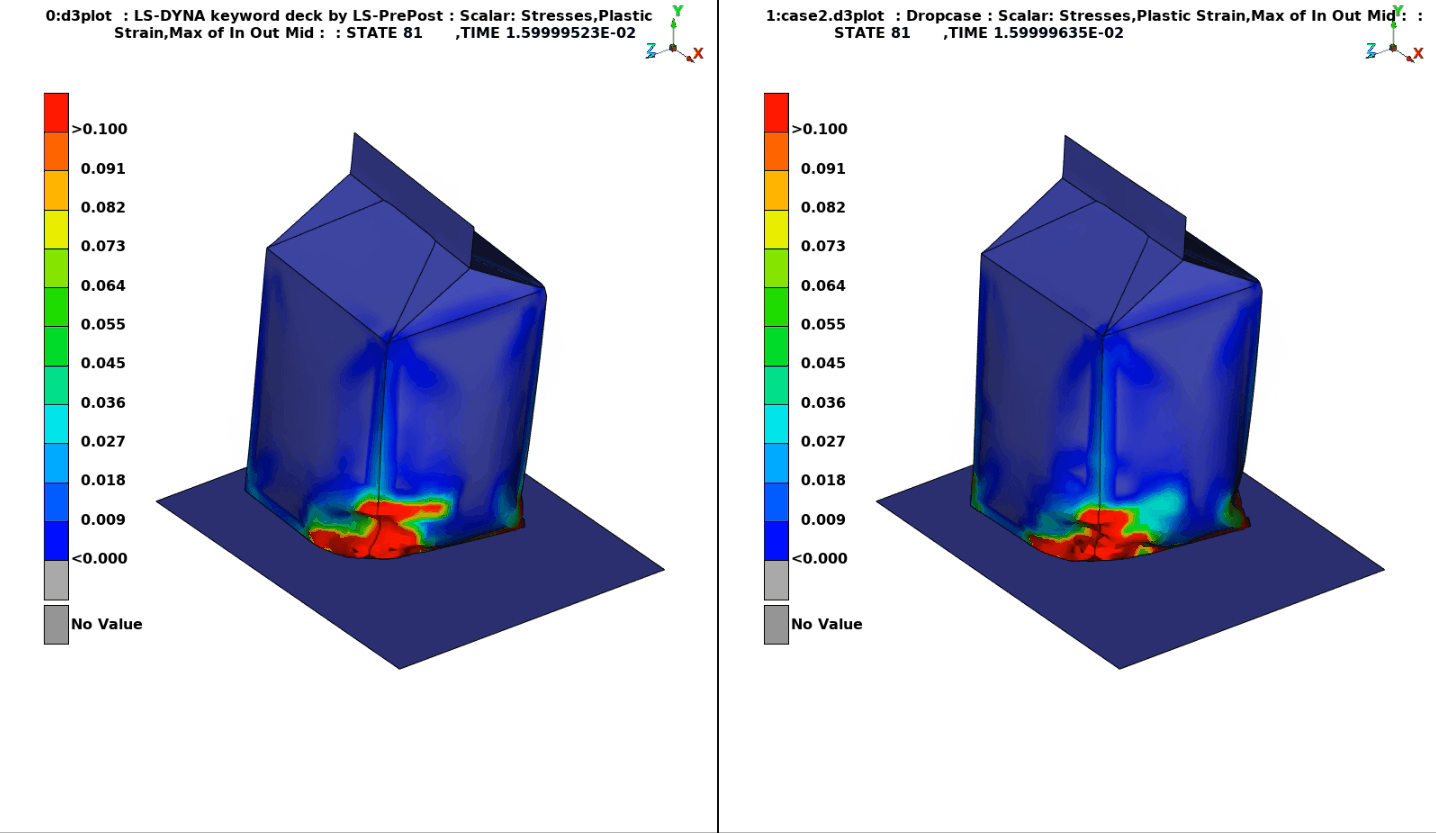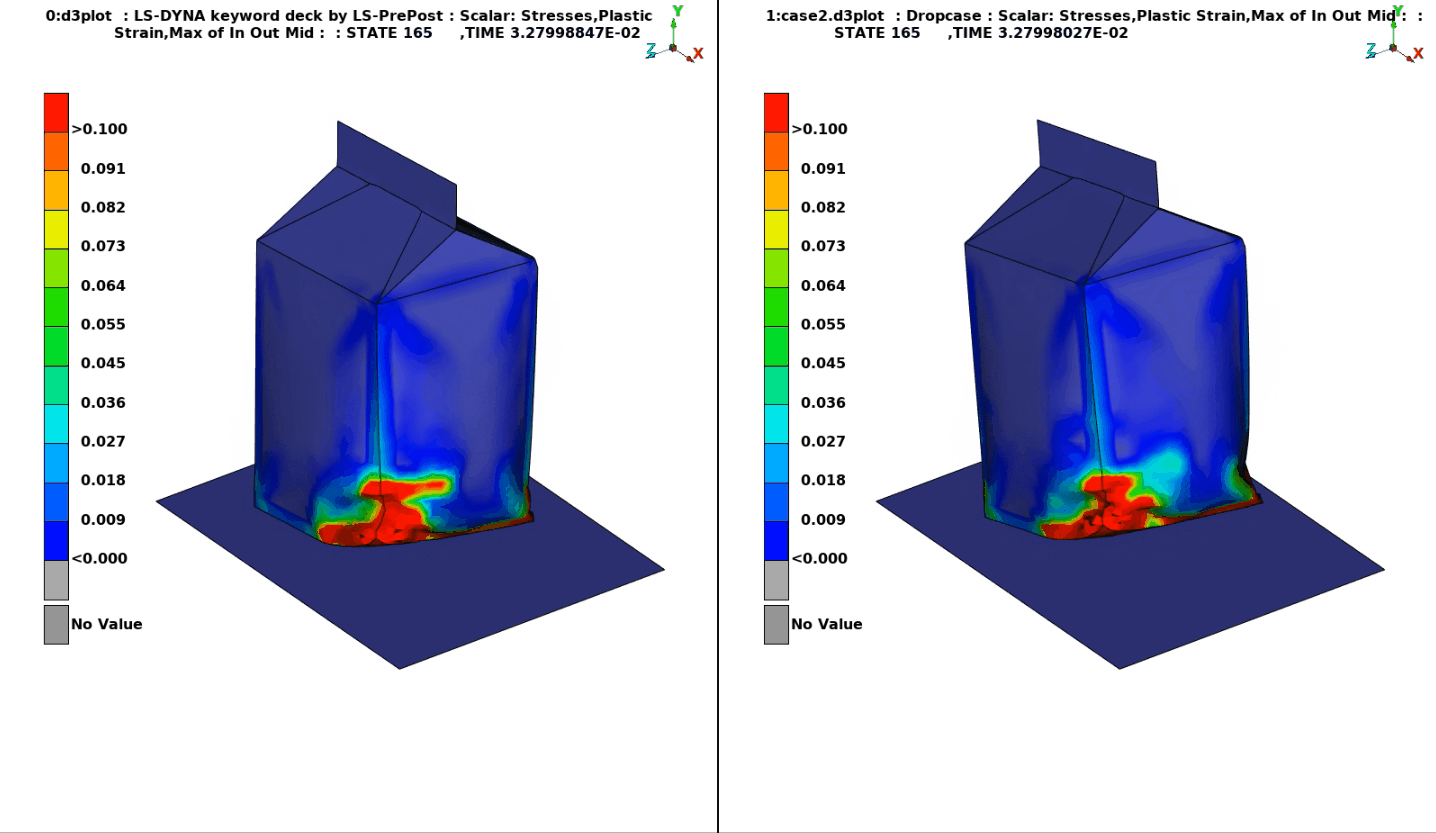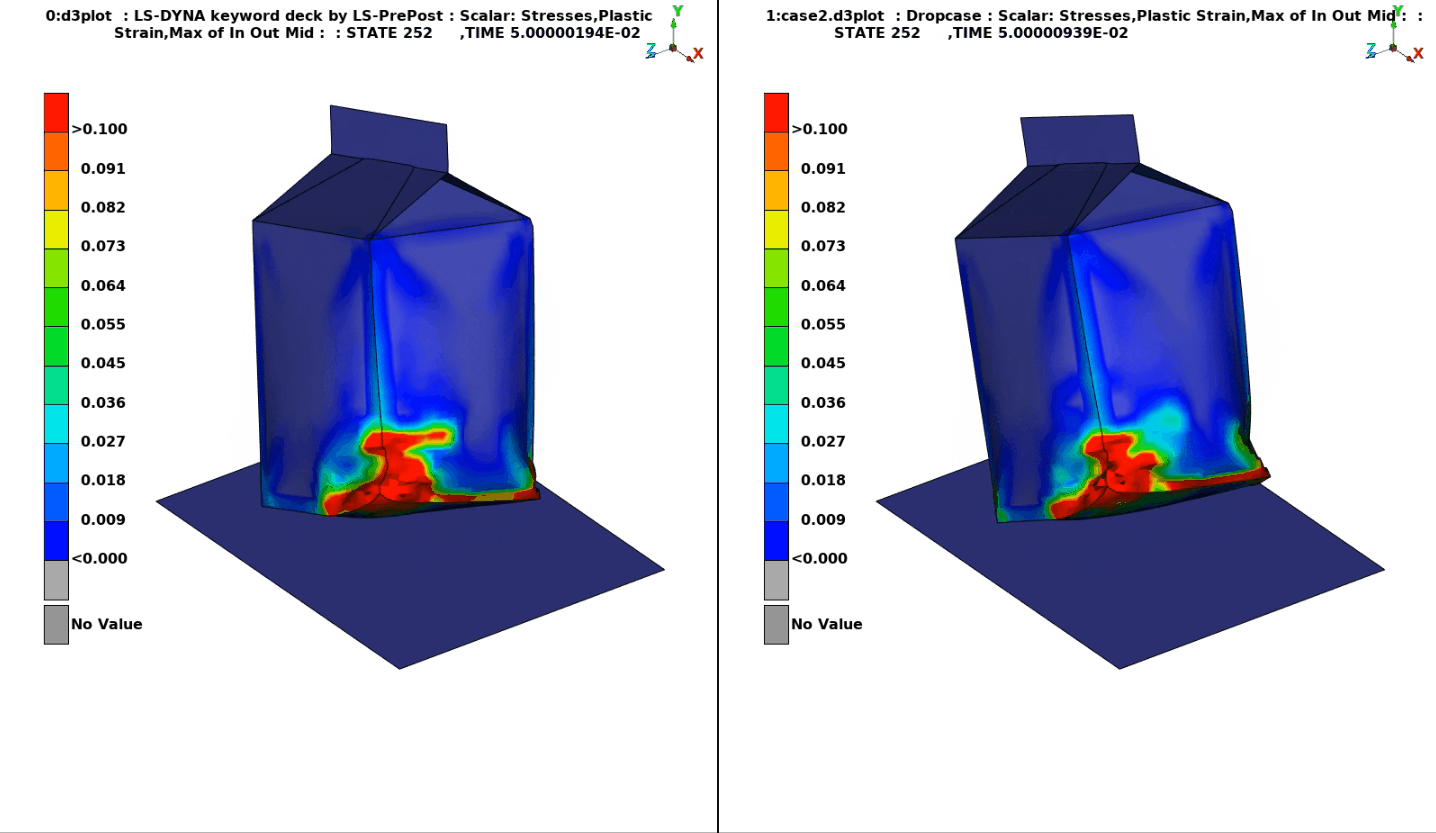
There is also a small difference in the folding of the package, best displayed in this animation of the plastic strains. But again, the differences are fairly small and could perhaps be related to the small difference in fluid mass between the two models.
Computational resources
If we compare the simulation times for the two modelling approaches, it can be noted that the DES solver is significantly faster to use in the drop simulation. Why? Well, a problem involving only spherical rigid bodies is much easier to solve. It is possible to make the implementation regarding for instance the contact search in such a scenario very efficient, compared to for instance solving the true physics of water with an equation of state.
| Model | Settling simulation | Drop simulation |
| DES | 21 min | 27 min |
| SPH | 22 min | 9h 14min |
In conclusion
So to sum up, if you want to model a structure subjected to a fluid-like loading, the computationally efficient DES method could be a viable option. It does, however, require some additional work to make it feasible, such as calibrations of non-physical parameters, scaling of particle densities, and particle generations in a closed volume followed by a settling simulation in which some tricks are applied. One must also consider if the rigid sphere representation is valid for the application in mind. For example, what happens when we want to model a viscous fluid? In this particular application however, it is likely to believe that the results are more a function of the amount (mass) of liquid applying a pressure during the drop. So for a faster development in which many design evaluations are made, the DES method could serve as a good enough loading option.
The SPH model, on the other hand, is much simpler to set up, because the parameters involved have a physical meaning. And also, the filling tool in LS-PrePost is easy to use to get the desired amount of fluid in the package. Perhaps this method is preferred for the final validation stage?
To learn more
Simulations have time and again proven to be a cost-effective product development tool that avoids costly tooling redesign. We have the software and knowledge required so that you may learn to perform these simulations yourself. We will guide you all the way, including training and support. To learn more, please contact one of our technical experts listed on this page.